排列组合是我们考试中很重要的一块内容，也是分值占比较大的一块。奈何这一块的题型多变，形式复杂，出题人变着花样玩儿我们。我们往往找不着规律，很难下手。

其中有一块内容很有意思，大家差不多都知道答案的样子长啥样，但往往又容易搞混，不知具体该选择哪一个。这就是“分房问题”。

例如：3个人随机进入5个房间，共有多少种方法？

这种问题的答案往往是这样的：

很多同学都能排除其他选项，但都搞不清楚，到底是应该选A还是选B？今天我们就来把这个问题好好地讲讲。

1，认识一个人，要多层次、多角度、多方面去观察、思考。同样的，我们做一种类型的题，要想搞清楚里面的门道，也要掌握不同的解题方法。

对于分房问题，因为模型比较简单，我们打算讲两种方法。当然，每种方法，我都会用2道题来让你深刻理解。

一、首先我们来看最正经的“分房问题”：如下

3个人随机进入5个房间，共有多少种方法？

假设我们现在让第一个人来选择进入房间，那这个人有多少种进房间的选择呢？很明显，他有5种选择，他想进哪个房间都可以，所以他有5种选择方案。

根据乘法原理，第一个人选择好以后，事情还没有完成，我们还需要第二个人和第三个人完成选择，也就是第2步和第3步。第2个人和第3个人都有5种选择方案，所以最终的结果就应该是：

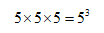
在这道题中，人是活的，房间是死的。人具有选择性，而房间是被选择的。所以谁具有选择性，谁就应该骑在别人头上。谁是被选择的，谁就应该“被压迫”。

人具有选择性，所以人的数字应该在上面。房间不具备选择性，所以房间的数字应该在下面。所以答案是：B。

二、上面那道题是“正宗”的“分房问题”，下面我们换个场景，换个数据来试试，看我们能否快速地做出答案。例如：

10个人坐公交车，经过8个车站，中间没人上车，请问下车方式有多少种？

这个和上个题目很类似，其中人是具有选择性的，站点是被选择的，所以人的数目要“骑上去”，站点的数目要“蹲下来”，所以答案就是8的10次方。

三、其他的类似于5个学生，每人只参加1个社团，共4个社团可选；5名运动员，参与4项体育运动，只能报名一项运动，等等，都是同样的思路。

我们来总结一下，这种方法的思路就是一句话：

谁有选择性，谁就是上流！

2，一个问题当然不止一种解法，不同的解法适合不同的人来理解。下面我们就还拿上面的两道题，从另一个角度来讲一讲。

四、仍然是最正经的“分房问题”：如下

3个人随机进入5个房间，共有多少种方法？

我们不再用选择和被选择的角度，我们换一个角度。我们来这样子思考：所有的房子能不能归到同一个人名下（家里好几套房子的娃儿，快闪开），当然是不能！那所有的人能不能归到同一个房间里面呢？也就是所有的人（3个人而已）能不能进入到所有的房间里呢？是可以的，这个时候，我们就说房间是个“大吃货”，它能把所有的人都吃到肚子里去。

人和房间比起来，房间算是“吃货”，因为它能容纳所有的人。而人在这里不是“吃货”，因为一个人不能同时进所有的房间。

“吃货”嘛，爱吃当然容易胖了，胖了自然就体重偏大，分量大自然就比较接地气一点，对应的数字就在下面啦！

因为房间代表“吃货”，所以它对应的数字5就在下面。所以答案是：5的3次方

②下面我们换个场景，换个数据来试试，看我们能否快速地做出答案。

例如：10个人坐公交车，经过8个车站，中间没人上车，请问下车方式有多少种？

在这道题里面，一个人不能在每一个车站都下车，但是同一个车站，可以让所有的乘客都下车，所以我们可以说，车站具有“吃货”的性质，所以车站的数字就在下面，所以答案是8的10次方。

③其他的类似于5个学生，每人只参加1个社团，共4个社团可选；5名运动员，参与4项体育运动，只能报名一项运动，等等，都是同样的思路。如社团是“吃货”，体育运动是“吃货”。

我们来总结一下，这种方法的思路就是判断：

谁要是吃货，谁就在下层！

品，你品，你细品！只顾着吃，不顾着学习和思考的，只能活在底层了！数学中蕴含着多么丰富的道理啊！

3，当然，上面两个方法都很简单，对应的题也很简单。现在我们来一个这类题型中偏难一些的，也就是学渣容易蒙对，而学霸容易做错的题。

看招：5个人竞选3名班干部（擦黑板专员、最后一排之排长、风扇开关总管），请问有多少种方法？

这个应该是3的次方还是5的3次方？答案是

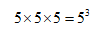
有同学不服气了，根据老师你，您刚才讲的选择性来说，人才有选择性，人的数字应该在上头啊。

不是这样的。不是说谁是活物，谁就具有选择性的！人有时候是身不由己的！

从选择性来说，人是不具备选择性的，你以为你想当最后一排的排长，你就能当上啊！在这里，班干部的职位是具有选择性的。比如风扇开关总管这个职位，我从5个人里选，我想让谁当，谁就当。所以在这里，职位反而是具有选择性的，所以职位的数字3应该在上头。

那从“吃货”角度呢？也不难理解，一个人可以同时兼任这3个职位，但是一个职位，可不能够让5个人都干。所以人在这里是具有“吃货”性质的，所以人的数字5是在下面的。

其他的比如还有：5个人争夺3项比赛的冠军。也是同样的道理，一个人可以同时拿3项冠军，但一个冠军不能是5个人都得。

4，总结一下，我们总共讲了两种思路：

谁有选择性，谁就是上流！

谁要是吃货，谁就在下层！

数学很枯燥，学着学着就容易恼羞成怒、心怀怨恨！因此学习过程中给自己找点乐子很有必要，这期的乐子如何？是不是讲出了硬核鸡汤的赶脚？欢迎点赞评论点在看！我们下期再见！