老师平常接触学生比较多一些,收集到的学生的问题也就多一些。因此,哪些问题是学生经常问到的,哪些问题是学生经常搞混的,老师还是略知一二的。今天我们就来讲一个排列组合中的分组问题。
话不多说,先上一道题瞅瞅:
将9个人分成3组,每组3个人,共多少分法?
既然是9个人平均分为3组,那必然是分成3、3、3,三个组。因此,我第一步从9个人里面选出3个人作为一组,第二步从剩余6个人里面选出3个人作为一组,第三步将最后3个人选走,作为第三组。即:
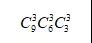
对吗?大错特错矣!!!
排列组合和概率问题存在着这样的“特点”:看似很正确的逻辑,往往里面有很大的缺陷。这道题的正确列法应该是:
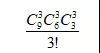
为什么要多除以一个3的阶乘呢?是因为这里面会有重复!我举个例子你就明白了。
假设我们用
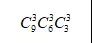
分出来的三组情况是:
(1,2,3)(4,5,6)(7,8,9)
也就是说,
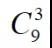
我选出来的是(1,2,3)
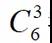
我选择出来的是(4,5,6)
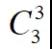
我选择出来的是(7,8,9)
可以吧?符合题意要求吧?
那我会不会
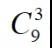
选出来的是(4,5,6)
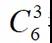
我选择出来的是(1,2,3)
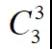
我选择出来的是(7,8,9)
这样分好的组就是:
(4,5,6)(1,2,3)(7,8,9)
那这个组和(1,2,3)(4,5,6)(7,8,9)不是一样的分组吗?情况一样,而且我这里只是分组,没有说给每个组编有号啥的。所以我们这道题就出现了重复。那出现重复,怎么消除,也很简单,就是几个字:
有几个组情况一样(指数字),就除以几的阶乘
在我们这道题中,有3个组情况一样(数目都是3个人),因此要除以3的阶乘,即3!(不是感叹号!不是感叹号!不是感叹号!重要的废话,说三遍!)。
上面那道题中,数学3来3去的,容易搞混,我们换个数字来做一下:
将9个人分成5人,2人,2人三个组,共多少分法?
首先,分人:
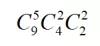
然后,有几个组情况一样,除以几的阶乘,在这里有两个组情况一样(都是2个人),所以除以2的阶乘:
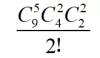
看,分组问题就是这么简单,先分数量,再看有几组情况一样,除以几的阶乘,从而消除重复。
还有同学说了,老师,这道题,我能不能先9个人中选2个人,剩余的7个人中选2个人,再剩余得5中个人选5个人,即:
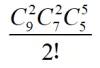
这样会不会结果不一致?哈哈,当然不会啦,你算一下就知道了,结果一样一样滴!
分组问题相对简单,一般不会直接考察,一般后面会再加上一个分配问题,综合起来考察。在这种题型中,一定要先分组后分配。只此一招,你就可以解决所有的这类问题,而且头脑不会混乱(不建议再学定向分组问题,容易搞混,学有余力的童鞋,就当我没说哈)。
来,整一道题试试呗:
将9个人分成3组,每组3人,然后分别执行甲、乙、丙三项任务,
共多少种方法?
如果是学习比较好的同学,上来就是定向分组:
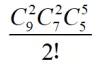
其逻辑是:9人选3人执行甲任务,剩余6人选3人执行乙任务,最后3人执行丙任务。但是有些同学会疑惑,老师,这样有没有重复啊(没有)?另外,我怎么才能知道有没有重复?这个和上面的那道题,有什么区别啊?
你看,混乱、迷惑就出来了。所以我不太建议学生同一类题学习很多解题方法,只要把一种解题方法学好了,弄懂了,就足够用了。多余的时间和精力,搞搞其他知识点或其他科目去。
因此我在这里只建议学习:先分组,后分配的方法。就两个步骤,①先分好组,避免掉重复;②再分配具体的工作或任务。
对于这道题,第一步先分组:
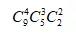
现在是分成了三个组,这三个组分别要去做3项任务,就相当于三个人坐3个座位一样,是个简单的排列,因此,乘以3!即可,即:
然后计算中省略啥的,自己搞就行了,思路永远保持清楚:先分组,后分配。
最后,这类题还有一种花样,也是把很多学生搞蒙了的,我们一并来解决一下,看一道题:
分配9个人执行甲乙丙三项任务,甲任务需4人,乙任务需3人,
丙任务需2人,共多少种方法?
牢记我们的思路:先分组,后分配。首先,先分组:
没有相同情况,不需要除以几的阶乘。然后,后分配,在分配的时候,这里要注意了,分组分出的4,3,2中,4人组的那个只能去执行甲任务了,3人组的那个只能去做乙任务,2人组的只能去执行丙任务。也就是分好组的那一刻,这些组的去向就定死了,所以后面的分配,我们也就象征性的乘以1的阶乘就可以了。
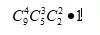
好了,分组问题就讲到这里了,欢迎点赞收藏点在看,不点不赞是坏蛋哟!我们下期再见!
老师寄语:
说实在的,生活和工作中,有很多问题都是有固定的解决方案的。需要创新性的解决思维的地方,极少极少。我们所能用于改变我们生活的,就是特定情况下,用固定的解决思路解决问题。
找到一个解决问题的方法,踏踏实实的按照这个方法的思路一步步执行下去,虽然有可能会慢一些、笨一些,但执行下去,一定会收获满意成果。
把时间用于琢磨技巧、窍门和捷径的人,注定是徒劳无功的,最终不但没有取得理想成果,还浪费了辛辛苦苦赚来的金钱,甚至搭上了宝贵的时间和注意力。
数学的学习过程中就存在一些问题,很多学生追求快速解题方法,找窍门,琢磨“三短一长选一长”、“三长一短选一短”啥的,就是不肯踏踏实实去琢磨清楚一个定理、一个公式。这些学生本质上是脑子糊涂,没有搞明白事情的重要性和重要顺序。
我们都清楚:做事情的难易程度和回报成正比。那些选择“走捷径”的学生,本质上就是认为找窍门比踏踏实实学习要简单,因为人的本性就是去难就易。但从上面的原则来看,我们选择了一条简单的事情,可想而知,回报(也就是成绩),自然就不再理想了。
所以,老师在这里奉劝各位考生,踏踏实实做好功课,耐心等待果实成熟的那一天。




