研线小课堂又开课了!一起来看看本期研线小课堂给大家带来的干货吧!
只要有心,生活中处处都可以发现哲理。这几天,老师在家里陪父母看《乡村爱情12》,颇有感悟。剧中,王木生参与赌石,花了5万买了一块石头,切开后是块好玉,当场被人50万买走。回去后,王木生就各种场合吹嘘自己眼光好、有天赋,自封玉石大师、极具天赋的投资家。
赌石和买彩票是一样的,买的就是一个概率(相信概率学的好的同学,不会去赌博和买彩票),运气好,说不定能发点小财,运气不好,那这钱也就是白扔进去了。这里面,中奖还是不中,运气的成本占99.9999%,个人能力基本上没有。
王木生赚的这50万里,基本上都是靠自己的运气赚的,能力的成分基本没有。所以,一笔生意赚了,如果运气成分占比要大于能力成分,那就赶紧收手吧。踏踏实实的打磨好自己的能力才是正道,把希望压在运气上,在关键时刻,运气一定离你远去!
数学学习过程中,来不得半点虚假。会就能做对,不会就做不对。有些同学去琢磨选项的技巧,琢磨速成的方法,这些都是在把自己一年的精力、时间和金钱,押注在虚无缥缈的运气上,最后考试怎么能考得好呢?谨记谨记!
Part.1
实数运算是我们学习的第一章,也是比较简单的一章,因为运算对于大部分学生来说,还是比较熟悉的,最大的差别就是你运算的快一些,他运算的慢一些而已。但其中还是有一些偏难点的计算题的,比如下面这道:
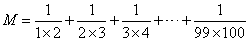
这类题一看,就不是让我们一步步老老实实地去算答案的,不然你算一天都不一定算出来。这种类型的题,类似于小学生学的奥数内容,样子看起来吓人,但有固定的套路,掌握了套路,问题就能迎刃而解。
观察一下,分母都是相邻的两个数相乘,而且,前一个分数分母中,相乘的两个数中最大的那个,是下一个分数分母中,相乘的两个数中最小的那个,依次往后排列。
这道题的解题方法就是直接将分数拆开,拆成两个分数相减的形式,例如:
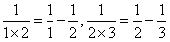
拆开以后,形状变了,但数值不变。因此,我们把所有的分数都拆开:
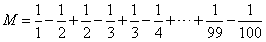
拆开以后,式子比原来长了两倍,但仔细观察我们发现:中间项,都可以消掉!就剩下首项和末项,因此,M的值就好算了。
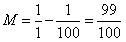
Part.2
上面是最简单的形式,我们来看稍微复杂点的:
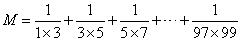
这道题每个分数中,分母是两个相差为2的数相乘,其他规律不变。那这个能不能按照上面的那道题的解法来做呢?我们来试试,首先我们先拆开一下试试:
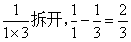
拆开后,发现数值大小发生了变化,变大了2倍,那我们可以乘以二分之一就可以了,我们拆开其他的试试看:
发现也是一样的增大了2倍,后面的都是拆开后,增大了2倍,要想保持数值不变,我们就在拆开后的整个式子的外面,乘上一个二分之一:
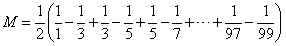
然后消掉中间项,答案就出来了:
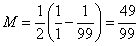
上面两道题,分母位置上相乘的两个数,相差分别是1和2。我们扩大一下相乘的两个数的差距,来看看是什么情况,例如:
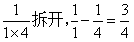
拆开后的结果比原数值增大了3倍,这个3正好就是分母位置上相乘的两个数相差的数值。由此,我们可以得出这类题的解法了:
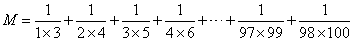
相差几,提出几分之一,然后直接裂项。
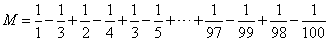
这就是我们说的,裂项相消法的做法。
Part.3
当然了,我们不会简单的就讲到这里,下面我们再增加一点难度,看你会不会跳进老师挖的坑里:
这道题和上面的那道题有些微的区别,我们做做看,首先还是:相差几,提出几分之一,然后直接裂项:
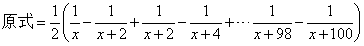
然后我们开始消除中间的项。这里要注意了,消除中间项的时候,一定要看清楚,有些项是消不掉的,尤其注意前几个和最后几个。比如这道题消掉中间项后的结果是这样的:
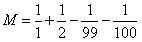
前面有两个项,后面有两个项是消不掉的。一定要注意!裂项相消法,在你裂出各项后,不要觉得马上答案就水落石出了,就得意忘形忘乎所以。一定要注意前边几个和后边几个,哪些能消掉,哪些不能消掉,做好这些工作,才算是完整掌握裂项相消法。
Part.4
最后,我们引申到分式中来进一步理解裂项相消法,在分式中,也有裂项相消法的运用,例如:
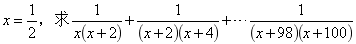
分母虽然不再是具体的两个数字相乘,但仍然是符合我们的规律的。分母位置相乘的两个数(在这里是式子)相差2,就提出二分之一:
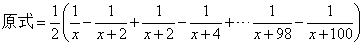
消掉中间项,得:
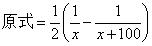
然后化简代入或直接代入算出结果即可。
好了,这期的讲解就到这里啦,对哪一块不够熟悉,想学习哪一方面的内容,欢迎在公众号留言,我们下期再见哈!
最后,送大家一句成吉思汗的话:不要因路远而踌躇,只要去,就必到达!祝各位研途顺利!
同学们一定要自己重新归纳总结老师提到的重点哦,我们下期见!




