恭喜你！没有因为标题不够吸引人就放弃打开这篇文章，而是选择谦卑地学习知识。这样的治学态度，才是真正可取的。

有一句老话是这样说的：

人败皆因懒，事败皆因傲，家败皆因奢。

一个人立身处世，不勤奋，不努力地往上走，肯定是不行的。尤其是对于有理想、有抱负的你来说。选择了考MBA，就是选择一条向上的通路，而往上走，没有走下坡路那样顺畅，有时候甚至要跪着往上爬，才能前进一小步。

不过，对于我们的未来，对于我们的梦想来说，实现梦想路途上遭受的一切艰难困苦都是值得的。上一个名校，读一个好专业，顺利拿到学位证，拥有更高的管理思想和格局。这对我们的未来来说，能起到很大的影响。而这一切的起源就是现在要好好学习，考上名校！

关于名校和普通学校的区别，知乎上有一个搞笑的问答：

名校和普通学校最大的差别在哪里？

好学校：老师觉得你很牛逼，你也觉得老师很牛逼。

差学校：老师觉得你是傻Ⅹ，你也觉得老师是傻Ⅹ。

虽然是开玩笑、调侃的话，但也算是说到了本质上。所以，为了成为未来更厉害的你，现在加油吧！

应用题中有这样一类题，它和集合问题相结合，而且集合往往都是相互有交集的那种，有时候是两个集合相交的形式，有时候是三个集合相交的形式。因为两个集合的形式比较简单一些，所以基本上我们做的也都是三个集合的形式。

我们先来看一道两个集合的真题：

（2011年）某年级60名学生中，有30人参加合唱团，45人参加运动队，其中参加合唱团而未参加运动队的有8人，则参加运动队而未参加合唱团的有（）

A,15人   B,22人   C,23人   D,30人  E,37人

这是涉及两个集合的问题，相对来说比较简单。对于这类涉及到集合的问题，我们有一个法宝，这位同学，你已经说出来了，那就是：韦恩图。我们来画一下这道题的韦恩图。

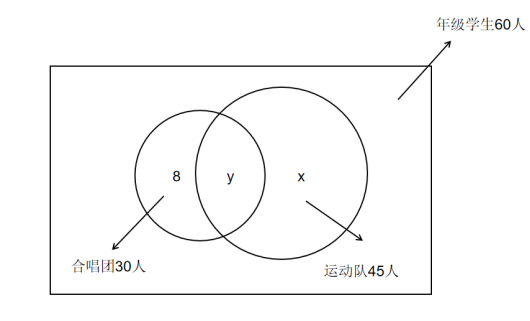
图中，老师已经在每个区域标注好了人数，未知的空白，也设上了未知数。我们这里有个规则，以防有些学生理解错误了。

在图形外边引出一个箭头的，表示这个图形的整个数量。比如这整个正方形的总人数是60人，整个合唱团的完整的圆，总人数是30人，整个运动队的完整的圆，总人数是45人。8，x，y分别就代表了他们所在的封闭图形的人数。比如y就代表两个圆中间相交部分的人数。

两个集合的应用题，比较简单，也很好做。对于这道题来说，式子很好列：

8+y=30

X+y=45

马上我们就能算出x是23人。

当然，只做简单的题，不是我们的目的。我们要掌握的是难题的解题思路和套路。下面我们就来看一道三个集合的题，也是真题哦：

（2010年）某公司的员工中，拥有本科毕业证、计算机登记证、汽车驾驶证的人数分别为130，110，90，又知只有一种证的人数为140，三证齐全的人数为30，

则恰有双证的人数为（）

A,45   B,50   C,52   D,65   E,100

首先还是第一步画图，我们来画一下韦恩图：

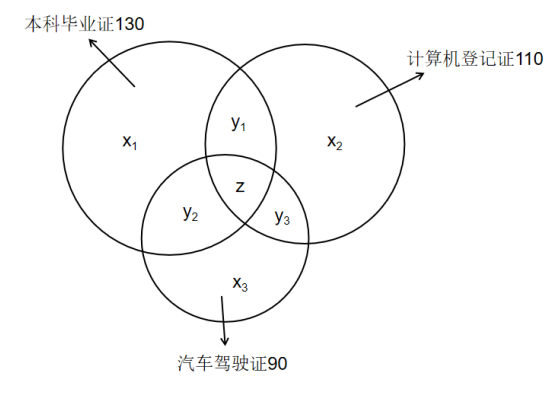
这里为什么没有像上面的题那样，画上一个大方框呢？（自己想哦！）这是三个集合的问题，所以交集的地方比较多，我们就用相应的标记标出来，以示区别。

我们用x1、x2、x3来表示只考了一个证件的人（哼！学渣！学酥！学粉！学末！学灰！）。用y1、y2、y3来表示考了两个证件的人（妥妥的学霸啊！）。用z来表示考了三个证件的人（学神，对我发誓，一定要说是李老师我教出来的啊！）。

这类三个集合的问题，其实刚接触的学生，是不知道如何下手的。老师先给大家分析一下，然后我们总结一个套路，以后我们就用这个套路来做这类题。

分析一：对于上图来说，所有的真实存在的人，我们这里用“真人”来代替，它是由三部分组成的：只有一个证的人，只有两个证的人，只有三个证的人，这些人都是真实存在的、没有重复的人。结合图上的标记，我们写成一个公式：

真人=一个证的人+两个证的人+三个证的人

真人=（x1+x2+x3）+（y1+y2+y3）+（z）

分析二：对于上图来说，有些人是“不存在”的，比如有本科毕业证的人+计算机登记证的人+汽车驾驶证的人。为啥这样说呢？因为这里面有重复！所以我们把这些人，用“真假人”来代替，它是由三部分组成的：1倍的只有一个证的人，2倍的只有两个证的人，3倍的只有三个证的人。结合图上的标记，我们写成一个公式：

真假人=1（一个证的人）+2（二个证的人）+3（三个证的人）

真假人=（x1+x2+x3）+2（y1+y2+y3）+3（z）

我们用这两个规律来做这道题试试：

真假人=130+110+90

一个证的人：x1+x2+x3=140

三个证的人：z=30

代入：130+110+90=140+2（y1+y2+y3）+3×30

y1+y2+y3=50

就这么简单，就用这两个规律的一个，或者两个一起用，绝对能解决问题！

以上就是我们归纳出来的规律，以后我们做题就用这个规律来做，保证能顺利解决大部分问题。还有解决不了的一小部分怎么办？放心，这类题不是出给你做的，是给高考的那帮孩子做的！

下面我们再来看一道题试试：

（2017年）老师问班上50名同学周末复习的情况，结果有20人复习过数学，30人复习过语文，6人复习过英语，且同时复习了数学和语文的有10人，语文和英语的有2人，英语和数学的有3人。若同时复习过这三门课的人数为0，则没有复习过这三门课程的学生人数是（）

A,7   B,8   C,9   D,10   E,11

首先，画韦恩图：

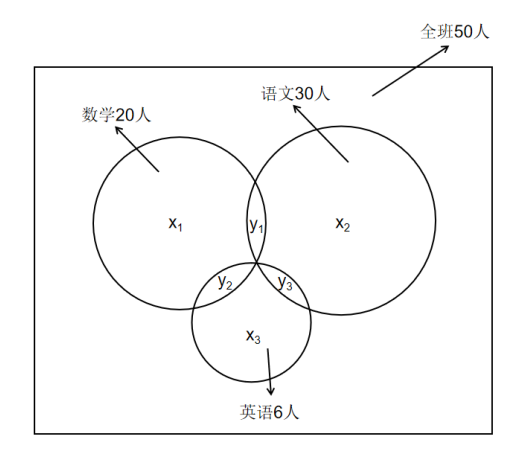
首先上公式：

真人=（x1+x2+x3）+（y1+y2+y3）+（z）

真假人=（x1+x2+x3）+2（y1+y2+y3）+3（z）

当然，这些都是在这三个圈里发生的故事，不包括方框的哈！（自己琢磨为啥出来个大方框，不做伸手党！）

其中：

真假人=20+30+6

y1+y2+y3=10+2+3

z=0

由此可得：

真假人=（x1+x2+x3）+2（y1+y2+y3）+3（z）

20+30+6=（x1+x2+x3）+2（10+2+3）+0

x1+x2+x3=26

真人=（x1+x2+x3）+（y1+y2+y3）+（z）=26+15=41

这些都是复习了功课的人，用全班人数减去这些人，就是啥都没复习的人（这些人都拉出去毙了）

50-41=9

好了，今天的专题就讲到这里，希望大家在书本上多找几道这样的题来做一做，加深印象。我们下期再见！