人生一世,谁都不是顺顺利利的,谁都会有犯错的时候,犯错是我们生命中必不可少的一部分。既然谁都会犯错,那人和人的区别就是对待错误的态度。有些人是立马寻找原因,改正错误。有些人是任由错误放在哪里,也不去解决,也不去寻找原因,吸收教训。对于前一种人来说,犯的错误反而成为下一步成功的基础。对于后一种人来说,往后的日子里,还会继续犯同类错误,还会在同一个地方摔倒多次。
人生有三种跌倒:乌龟式跌倒,不倒翁式跌倒,和朝圣者式跌倒。乌龟式的跌倒就是一旦跌倒,就不再翻身,只是仰躺着眼瞪天空,等待外力来帮扶一把;
不倒翁式的跌倒就是总是不停地跌倒而且常常是在同一个地方,但每次都不屈地爬起,然后换个方向,继续开始下一轮的跌倒和爬起;而朝圣者式的跌倒,因为心里有个坚定的目标,比如去冈波仁齐峰朝圣,所以虽然跌倒了,但每次跌倒的地方也都更接近目标。
愿我们每个人都能做朝圣者,让每一次跌倒,都能让我们更接近目标。
1
应用题中,我们经常会列出一个方程,方程里面是一个未知数,然后我们就能解出未知数的值。或者列出一个方程组,两个未知数对应两个方程,三个未知数对应三个方程,然后通过消元法,就能解出每一个未知数。这是我们常规的做应用题的方法。
但是还有一类题,其未知数的个数多于方程的个数。这类问题,我们一般称之为不定方程(组),不定方程(组)一般有无数组解,但题意往往要求我们求出其中的特殊解(一般为整数解)。对于这类题,常规的解法就失去了作用,那怎么解决呢?我们常常利用整除、奇数偶数、范围等特征来确定最后的答案。
先来一道题试试:
在年底的献爱心活动中,某单位共有100人参加捐款。经统计,捐款总额是19000元,个人捐款数额有100元、500元和2000元三种。该单位捐款500元的人数为()
A,13 B,18 C,25 D,30 E,38
我们的常规解法是设未知数,然后列出方程:设捐款100元、500元和2000元的人数分别为x,y,z,则有下列方程: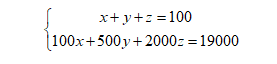
化简后:
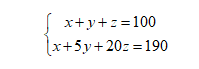
很明显,两个方程,三个未知数,你要让我通过消元法解出方程,我只能说:臣妾做不到啊!那怎么办?走一步是一步,我先消掉一个未知数再说,两个式子上下相减,得:
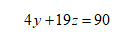
然后这个方程要想解出答案,是不太现实的,它有无数组解。可我们设的都是人数,人数肯定是正整数,那就好办多了,我们一个个试也能试出来。我们分别让z取1,2,3,4,5(为啥是这五个数呢,因为z再大点,y就得是负数啦),这里还有一个技巧,因为4y和90都是偶数,所以19z也得是偶数,所以z是偶数,所以z取值就为2,4。通过验证,可得在z为2,y为13时,为唯一的整数解组合。然后我们再代入求出x的值即可。
这是利用整数的一些性质来解决这类不定方程的一个案例,大家仔细琢磨琢磨哈!
2
上面是两个方程,三个未知数让我们求解的,就已经够我们头疼的了,还有更狠的呢!一个方程,三个未知数!不过,我们同样能解,但是,得借助不等式的一些性质。
下面看题:
在某次考试中,甲、乙、丙三个班得平均成绩为80,81,81.5,三个班得学生分数之和为6952,三个班共有学生()
A,85 B,86 C,87 D,88 E,90
还是我们的常规思路,先设甲、乙、丙三个班的学生人数分别为x、y、z。那根据题意,我们列出方程:
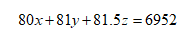
这,这,这,这让我,猎人抓刺猬,无处下手啊!那这类题如何做呢?这类题没有上面那道题的数字那么小,不适合用穷举法解决。那这时,我们就要利用不等式的一些性质,把要求解的东西的值给限制到一定的范围,然后再计算。我们把式子变化一下。
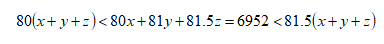
因为我们要求解的是x+y+z的值嘛,所以可以通过这个变化,给x+y+z计算出一个范围,这个式子计算一下就是:
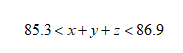
到这一步了,你还会说不知道答案是啥么?
3
不定方程在我们的考试中出现的很少,但也差不多过几年就有一个,这类题的特点就是看着很吓人,不知道怎么才能解出答案。但解题方法很容易掌握,说破了就简单了。
下面我们看一种不定方程的另一种题型。
某单位年终共发了100万元奖金,奖金金额分别是一等奖1.5万元、二等奖1万元、三等奖0.5万元。则该单位至少有100人。
(1)得二等奖的人数最多。
(2)得三等奖的人数最多。
这是一道条件充分性判断题,是看哪个条件能推算出来该单位至少有100人。上面的两道题,都是最终求解出一个整数的解。而这道题求的是一个范围,怎么做呢,我们来做做看。
首先设领1.5万元,1万元,0.5万元的人数分别是x、y、z,(年终奖够丰厚得呀,老板,看这里,这里,我也要!)根据题意有:
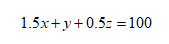
这个是题目中给的已知条件,最终就是看条件(1)和条件(2)哪个能推出来x+y+z≥100。我们来看条件(1),得二等奖的人最多。条件(2),得三等奖的人数最多。不管得二等奖和三等奖的人数是什么情况,我们的当务之急就是建立上面的式子和x+y+z的关系,因为我们的目的就是x+y+z。那我们把上面的式子给变化一些,硬凑出一个x+y+z。
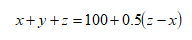
现在x+y+z凑出来了,而且尾巴上还带了个100,好像和100有些关系了。既然要求最少100人,那么只要(z-x)≥0不就可以了吗?即z≥x就可以了。我们看条件(1),只提到了y最大,和我们的推论没关系,也推不出z≥x。条件(2)中,z最大,那z≥x是肯定成立的,因此这道题条件(1)不充分,条件(2)充分。选B。
好了,不定方程的内容,我们就讲到这里了,希望下期还能在这里遇见你,我们一起进步、一起成长,迎接考试,迎接金榜题名的那一天!




