我一向有个看法:若是某件事儿你觉得需要努力、需要坚持才行,那这事儿基本上从一开始就注定做不成了。因为需要努力、需要坚持,说明你骨子里不愿意做啊!
我很早就想明白了这个道理。于是,我磨炼出了不需要坚持就能做好事情的两个技巧,这就是今天我要跟你分享的内容,这两个技巧分别是:
1、在开始做事情前,先为这件事赋予重大意义。
一件事情,如果我们觉得做起来没有意义,我们是不会有动力去做下去,并且乐此不疲的。你观察一下小孩子,他们玩游戏的时候就是很专注,也不会嫌脏嫌累,只会觉得很好玩儿,而且玩儿的停不下来。所以,如果你要想把一件本来心里有些抗拒的事情好好做,认真做下去,就要给这件事情赋予重大的意义,让这件事显得很好玩儿。比如,你要想象等你考上了研究生,你的生活会怎么转变,你的家人会如何奖励你,你的男神女神会如何对你刮目相看,你的未来会更加有希望。多去想象一些这类东西,比你苦哈哈的做两道题,管用多了。
2、思考如果不做这件事,会有哪些负面意义。
有时候,我们做事情,不单单是因为兴趣、动力啥的,还有恐惧的原因。人在恐惧的时候是会爆发出巨大能量的,给你的脑袋一个恐怖的画面,会吓着它的。比如,想象你没有好好学习,最终没有考上研究生,自己垂头丧气,还得再来一年,还要在家人朋友面前抬不起头来等等,这会让你的大脑时刻处于危机之中。这也是很好的刺激自己的一种方法。
1
数字问题,是排列组合题中一类比较有代表性的题。这类题需要注意的事项比较多,比如末位为0为5,奇数偶数的问题,比如首位不能为零的问题等。今天我们就把常见的数字问题都列出来,统一做一遍,彻底掌握数字问题的做法。首先看一道简单的题:
由0,1,2,3,4,5这六个数字:
(1)可组成多少个无重复数字的三位数?
(2)可组成多少个允许有重复数字的三位数?
第一问:三位数中,其中首位最特别。为啥?因为首位不能为0啊!所以我们从1,2,3,4,5中选择一个放到首位,总共有5种选择方法。然后再安排十位和个位,分别有5种和4种选择方法。所以总计有5×5×4=100个。
第二问:允许有重复数字的三位奇数,则末位为1或3或5。当末尾为1时,首位可以在1,2,3,4,5中任意挑选,十位在0,1,2,3,4,5中任意挑选,所以共计有1×5×6=30个。同理,当末位为3或5时,也各有30个,所以共计90个。
这道题相对来说是比较初级的数字问题,我们来点有难度的:
从0,1,2,...,9这十个数字中任取五个不同数字:
(1)正好两个奇数,三个偶数的不同取法有多少种?
(2)至多有两个奇数的取法有多少种?
(3)取出的数中含5但不含3的取法有多少种?
第一问:分两个步骤完成,先在1,3,5,7,9这五个奇数中任取两个;再在0,2,4,6,8这五个偶数中任取三个。用乘法原理,总取法有
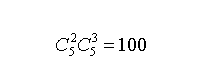
第二问:用加法原理,可涉及为三种方案:两奇三偶,一奇四偶或五偶,所以总取法有:
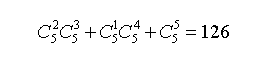
第三问:先将5取出,再在0,1,2,4,6,7,8,9这八个数字中任取4个即可,因此不同取法为
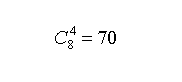
2
上面的是两道比较简单的数字问题,下面我们来看两道正常难度的数字问题:
由0,1,2,3,4,5:
(1)可组成多少个无重复数字的不同三位偶数?
(2)可组成多少个不同的三位偶数(允许有重复数字)?
(3)可组成多少个能被5整除的三位数(允许有重复数字)?
第一问:三位偶数,则个位为0,2,4。
当个位数字为0,百位从剩余的5个数字选,十位从剩余的4个数字选,有5×4=20种。
当个位数字为2,百位从剩余的4个非0数字选,十位从剩余的4个数字选,有4×4=16种。
当个位数字为4,百位从剩余的4个非0数字选,十位从剩余的4个数字选,有4×4=16种。
共计20+16+16=52种。
第二问:同样的,三位偶数,个位为0,2,4。不过,这次允许有重复数字了。
当个位数字为0,百位从5个非0数字选,十位从6个数字选,有5×6=30种。
当个位数字为2或4时,情况和个位数字为0时一样,所以分别都是30种。
共计30+30+30=90种。
第三问:能被5整除,则个位必须为0或者5。
当个位数字为0,百位从5个非0数字选,十位从6个数字选,有5×6=30种。
当个位数字为5,情况和个位数字为0一样,也是30种。
共计30+30=60种。
3
上面做了几道数字题,都是一些数字问题的常见类型,那真题中是什么考察形式呢?真题一般不会考察常见的类型,那是不是常见类型我们就不学习了?不是的,这是基础,没有基础,哪有高楼大厦?真题一般会在很普通的面貌下,设置一些坑,让你不知不觉中就掉进去,我们来看一道2014年的真题。
(2014)用0,1,2,3,4,5组成没有重复数字的四位数,其中千位大于百位,百位大于十位的四位数个数是()
A,36 B,40 C,48 D,60 E,72
这道题首先肯定是已经隐含了首位不能为0的条件,其次,这里面说千位大于百位,百位大于十位,这个应该怎么去做?
有些同学已经想到要用穷举法,让千位分别为5,4,3,2。但这思路只能算是正常的思路,对于解决这道题还是不够的,因为我们看一下答案,都是好几十,穷举法一般不会让我们穷举出很多数字,所以穷举法的思路不可取。
那我们应该怎么办?我们在学习排列组合这一章的时候,常说要谁特殊先安排谁,这里千位、百位、十位比较特殊,但是我们不知道如何下手,那这时候,其他位置,也就是个位反而是最特殊啊,因为它不涉及到被限制范围。
那个位没有限制条件,就可以从6个数字中任取了,想取谁取谁(老师也憧憬着想娶谁娶谁,那多好!),所以个位有6种取法。那其余3个位置,怎么办呢?那我先不管,我先取出来3个数再说,从剩余的5个数字中任取3个。合起来就是
什么?老师,这怎么就完了?怎么5个里面任取3个就结束了?再说,首位不能为0还没有考虑到呢,万一这任取的3个数字中含有0可咋办捏?别着急,且听老师慢慢给你道来!
从5个数字中任取3个,这三个数字是不是有大有小有中间啊?那大的是不是只能去千位,中间的数字只能放在百位,小的数字只能放在十位啊?也就是取出的那一瞬间,它们的去向就决定了。
有0也不怕,0最小,就算取出来,也只能放在十位,首位是不可能放0的,最小也是2。看,真题就是这样,出题人时时刻刻想着绊你一跤,坑你一下,你说,不好好学习,能行么?
好了,这期的内容我们就到这里了,欢迎大家阅读、学习和交流,我们下期再见!




