如果我们某天回到家,发现钥匙丢了,那我们怎么办?我们会不会在锁头上反复寻找,反复琢磨,去找寻钥匙?不会的,因为既然没有钥匙,那就说明打开锁头的钥匙,一定不是在锁头上,一定是在其他地方。在锁头上再怎么寻找,也很难找到钥匙的。所以,当你遇上一个被锁住的锁头时,第一时间要想到的是,去别的地方寻找钥匙。
你瞧,当我们遇到任何问题的时候,也是一样的道理。既然那是个需要被解决的问题,它就好像是个被锁上了的锁头,那么解决方案就像是钥匙一样,一定不在锁孔里插着,一定是在别的什么地方。所以,当我们尝试解决任何问题的时候,只盯着问题看,盯着问题想,盯着问题找解决方案,通常只能是以无奈告终的。
对应到我们的学习中,也是一样的道理。数学学习的不好,题不会做,只是在题上瞎琢磨,是很难把题解答出来的。正确的做法是,找来书本,把相应的知识点、概念、公式,仔仔细细、逐字逐句地读上两遍。把概念搞清楚,把公式记明白,把推理过程自己推演一边,真正地深刻理解了知识点,做题才能有思路啊!
1
韦达定理是一元二次方程中的内容,是由求根公式推理出来的,我们再来简单地回顾一下。
求根公式是这样描述的:一元二次方程ax2+bx+c=0的根的表达式为:
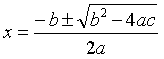
我们将两个根分别相加和相乘后,就得到了韦达定理:
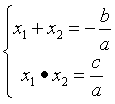
韦达定理反应的是根和系数之间的关系,而根和系数,是一元二次方程的全部内容。考察的时候,要么考察根的情况,要么考察系数的情况。如果要把根和系数结合起来考察,那就少不了韦达定理在中间做“红娘”了。
韦达定理在每年的考试中出题比例较低,一般是和其他知识点结合着考察,直接考察韦达定理的几乎没有,一般考察韦达定理的变式的比较多。今天我们就把常见的几种考察形式和常见的一些考察题型给大家列出来,让大家把这块的内容学扎实了。
首先来一道比较综合的题吧,几乎涉及到了韦达定理的绝大部分变式。看题:

这道题没有直接考察两根之和与两根之积,而是写成了两个根的复杂变式,那要想用到韦达定理,就要把变式进行改变,变成两根之和与两根之积的形式。然后再运用韦达定理,就可以直接带入了。
首先,我们根据韦达定理,得出根与系数的关系为:
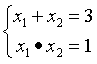
然后我们把四个变式通过变换,变换成我们需要的形式:
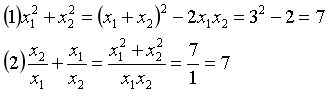
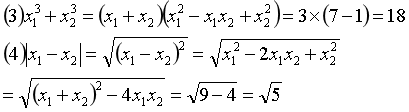
2
上面是直接考察韦达定理的变式的问题,比较简单粗暴,是我们刚开始学习韦达定理时必须要经历的做题过程。
但实际上,真正考察韦达定理的题,会比较绕一些。比如我们不直接求两根变式的值,我们反过来求方程中未知量的值,或者求未知量的取值范围,或者根据未知量来求根的正负性等问题。下面我们分别来看几道题。
这道题比较简单,先撂出韦达定理:
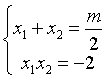
代入到题中的式子中,得:
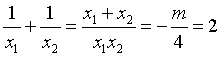
由此,我们可以得出,m=-8。很多学生以为到这里,就结束了,实际上也真的是结束了,做完了(那李老师,你到底要说啥?)。但这里,我们其实缺少一种意识,就是忘了考虑判别式。因为题中说,方程的两根啥啥啥的,意思就是方程有两个根,相等不相等不知道,但有两个根,那我们首先就要想到判别式大于等于0,于是有:
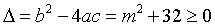
这里其实m是任意实数都可以,没有再求出m的一个限制条件,所以求判别式大于等于0其实是多此一举。但我们一定要有这种意识,一定要把判别式考虑进去,因为有时候很多题就含有这种隐藏条件,你要是一个不小心,忽略了,那就出错啦!
我们来做一道和上面这道题类似的题,但是隐藏了判别式的考察内容,看题:
已知关于x的方程x2+2(m-2)x+m2+4=0有两个实数根,且这两个根的平方和比两根的积大21,则m=:
A,17 B,-1 C,17和-1 D,1和-17 E,-17
首先,撂出韦达定理:
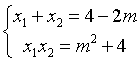
根据题中描述,我们列出式子并变换形式:
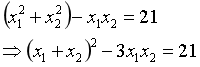
将韦达定理代入,可得
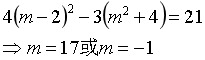
如果你做到这里就直接选答案,那就错喽,还少一个判别式呢!
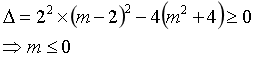
在这里,判别式往往还能再将m的值限制一下,少了这个步骤,分数就跑喽。所以一定要存在这种意识,多考虑一步判别式。
3
有的时候,我们不只是考察题中未知量的值,还考察他们的范围,或者通过未知量的范围或值的大小,来判断根的情况,我们分别都来看道题。
已知方程x2-2x-m有两个相等的正根,则m的取值范围是:
A,m>0 B,m<1 C,-1<m<0 D,m<-1 E,0<m<1
那既然涉及到两根,就一定涉及到判别式和韦达定理,我们列出式子:
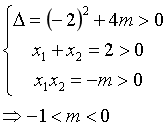
再来看一道考察判断根的情况的一道题:
当m<-1时,方程(m3+1)x2+(m2+1)x=m+1的根的情况是
A,两负根 B,两异号根且负根绝对值大 C,无实根 D,两异号根且正根绝对值大 E,以上结论均不正确
既然考察根的情况,那首先第一步,我们要考察根是否存在,考察根是否存在,那是判别式的事儿:
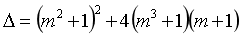
当m<-1时,判别式大于0,所以方程两个根是存在且不相等的。其次,我们再通过韦达定理,来具体判断根的正负性问题:
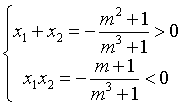
两根相乘小于0,那肯定是一正一负;两根相加大于,那肯定说明正根绝对值大嘛!所以选D喽!
好了,这期的内容,我们就讲到这里啦,希望各位同学疫情期间在家沉下心来,好好学习,我们下期再见!




