面对麻烦,能解决就去解决,这是能力;面对麻烦,不能解决就承受,这是坚韧。
正是出于这个原因,坚决不抱怨成了我自己一直坚持的原则。抱怨,是无能、无奈的表现,是这个世界上最强的负能量,它会让一个人失去挣扎的能力,失去承受的坚韧。所以,要彻底戒掉抱怨的恶习,唯有不抱怨才是基于自己的能力和坚韧的表现。
抱怨的害处,并不仅仅在于浪费时间,也不仅仅在于那样会暴露自己的无能;它真正的害处在于,它会让你不由自主地放弃挣扎。
心理学家早就知道这事儿,并且详细地论述过:说话,对每个人来说,其实都是“大脑重塑”的过程。我们每个人都倾向于不由自主地“扮演”我们向别人描绘的那个样子,直至成为那个样子。
你观察一下就知道了,那些向你抱怨的人,说着说着就开始进入“表演”状态,他们很投入的,他们需要你的同情,他们需要全世界的同情和“理解”;为了让你同情,为了让全世界同情,他们就会不由自主地扮演“一个其实更惨的角色”,演着演着,别人还没怎么样,自己先信了,不由自主地任由自己变成那个“更惨的角色”——你想成为一个“更惨的人”吗?开始抱怨就可以了,多简单!
1
应用题中的售货问题,是和商业管理最接近的一类题型。为什么呢?因为商业的最根本驱动力就是要盈利嘛!要盈利就要涉及到成本、进价、售价、盈利和平均成本等问题。我们的数学试题中,直接涉及到商业管理的比较少,而应用题是最接近商业管理模型的。今天,我们多做一些应用题中的售货问题,这对我们提高数学水平和提高商业敏感度,都有很大好处,下面,我们就来好好地做几道题。
要想做好应用题中的售货问题,就要掌握基本的商业逻辑,简单表述如下:

这是解决售货问题要掌握的最基本的逻辑,也是列式子所需要的等量关系。一定要记好喽!下面我们来看道题:
(2001年)一商店把某商品按标价的九折出售,仍可获利20%,若该商品的进价为每件21元,则该商品每件的标价为()
A,26元 B,28元 C,30元 D,32元
进价和利润率有了,售价不知道,题中说售价是标价(标牌价格,就是李老师3块钱买了双袜子,牌子上却写着:建议零售价888元!)的九折,那我们就设标价为x,售价就是0.9x。根据利润率的公式,可得:
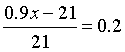
解得,x=28。你看,真题也不是很难吧?我们只要掌握了基本的商业逻辑公式,做这类题就没有什么大问题。
2
我们接着再来看一道真题:
(2009年)一家商店为回收资金,把甲、乙两件商品均以480元一件卖出,已知甲商品赚了20%,乙商品亏了20%,则商店盈亏结果为:
A,不亏不赚 B,亏了50元
C,赚了50元 D,赚了40元 E,亏了40元
两件商品的售价都给了,利润率也都给了,就差两个商品的进价了,只要算出了进价,售价和进价的差就能知道是赚了还是赔了。
我们假设甲商品进价为a,乙商品进价为b,则根据题意有:
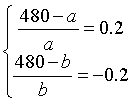
解得:a=400,b=600。也就是甲乙的进价(或成本)是1000元,卖出了480×2=960元,那自然是赔了嘛!赔了40元。所以应该选E。
我们再来看一道条件充分性判断题:
售出一件甲商品比售出一件乙商品利润要高。
(1)售出5件甲商品,4件乙商品共获利50元。
(2)售出4件甲商品,5件乙商品共获利47元。
这道题,很明显,具有选C的潜质,因为条件(1)和条件(2)长了一张要“联合”的脸型啊!题中没有说甲乙两商品的进价和售价,所以单纯来看,并不知道谁的利润高,所以这道题,我们只能联合。
但这里我们就没必要再去设出甲乙的进价和售价了,因为题中考察的是利润,最终也是“获利”多少多少,所以,我们直接设甲乙单件的利润就可以了:假设一件甲商品的利润是x元,一件乙商品的利润是y元。联合后,根据题意有:
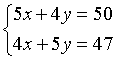
正常情况下,接下来我们应该求出x,y,然后比较大小即可。但如果你平时计算比较有经验,这里就让上式减去下式就可以得到,x-y=3。那就很明显,甲商品的利润高嘛!所以答案选C。
3
上面的几道题,基本上都是考察出售单件商品,我们一般考察它的进价、售价、利润和利润率。但实际上的商业社会,大部分都是成千上万件的单子,那这个时候,因为单子多了,就要涉及到涨价或降价的问题,还要涉及到总利润的问题等等,因此问题就复杂一些。
不过,在我们这里,模型仍然是简化了的,单件商品的问题,要想转化成多件商品的问题,就是在原有公式的基础上,多加上“销量”这个元素而已。

下面我们就来看两道题,感受一下大订单下的商业社会:
某商店将进货价为10元的商品按每个18元出售时,每天可以卖出60个。经调研发现,若在此基础上,每降价1元,则每天可以多卖出5个;每涨价1元,每天要少卖出5个。则为了获得最大利润,售价应定为每个
A.20元 B.17元 C.16元 D.15元 E.14元
再来看一道考察判断根的情况的一道题:
当m<-1时,方程(m3+1)x2+(m2+1)x=m+1的根的情况是
A,两负根 B,两异号根且负根绝对值大 C,无实根 D,两异号根且正根绝对值大 E,以上结论均不正确
利润=(售价-进价)×销量,现在进价是知道的,售价暂时不知道定位到多少合适,销量是随着售价变化的,而利润是我们最终要考察的对象,因此,这是一个关于售价和利润的函数类型的题。
我们设价格调整为x,则售价为18+x,所以,销量就变为60-5x(x若为正,即涨价了,销量下降;x若为负,即降价了,销量上升)。假设利润为y,则可得
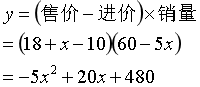
我们最终是为了获得最大利润,体现在这个式子里,就是求这个一元二次函数的最大值。这里容易知道,函数图像是开口向下的,有最大值,无最小值。
那我们这里需要求出最大值是多少么?完全没必要,因为最终是求定价多少。所以,求出x的值就可以了,当函数取得最大值的时候:
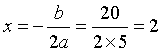
也就是,若要取得利润最大,则往上调价2元,即售价定为18+2=20元。选A。
好了,这期的内容,我们就讲到这里了。疫情马上就结束了,我们快要结束这段艰难的历程了,希望过段时间,我们线下相见的时候,都已成为了更好的自己。




