什么才是一个人最宝贵的财富呢?金钱?时间?都不是,注意力才是每个人都拥有的、最重要、却被人忽视了的宝贵财富。
钱不是最重要的,因为它可以再生;时间也不是最重要的,因为它本质上不属于你,你只能试着与它做朋友,让它为你所用。你的注意力才是你所拥有的最重要、最宝贵的资源。所以,你必须把最宝贵的注意力全部放在你自己身上。
注意力是我们内在的选择,它不像时间是游走在我们身体之外的东西,而是可以通过我们的控制完全为我们服务的。最终,你的一切价值,都是你的注意力的产出。而且,更为关键的是,一个人的注意力,很可能是唯一能够称得上是“与生俱来”的,有产出能力的资源。
那注意力要放在自己的哪儿上呢?答案明确而又唯一:放在“成长”上。
成长才是根本关键。选择是否做一件事的判断标准有一个就足够了:我选择的事能不能让我积累更多的能力?
这里有个陷阱:很多人在做选择的时候,考虑的是,在这个选择之后,我过往的能力能否用得上?这是“终点式思维”,不是“里程碑式思维”。正是因为这样想了,所以大多数人习得新能力的可能性越来越低。因为他们不知不觉已被自己的已有能力禁锢了。
真正正确的思考方式应该是:在这个选择之后,能帮我完善哪个已有能力,能让我获得什么新能力。
1
行程问题在应用题中,属于偏简单一些的问题,因为我们从小学就开始大量的做这类应用题,已经非常熟悉了。但我们小学做的都是偏简单的,在我们的考试中,行程问题有时候题目会比较难一些,所以,我们这里有必要拿出几道难题来看看,到底是难到了哪里?过程简化后,是不是和简单题没啥区别呢?
快、慢两列车的长度分别为160米和120米,
它们相向行驶在平行轨道上。若坐在慢车上的人见整列快车驶过的时间是4秒,那么坐在快车上的人见整列慢车驶过的时间是()
A,3秒 B,4秒 C,5秒 D,6秒 E,以上结论均不正确
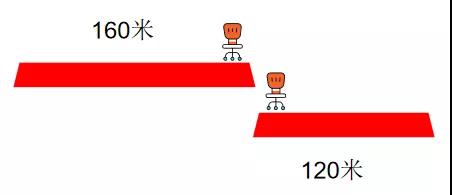
很多同学会觉得,求时间得知道路程和速度。但这里两辆车的速度都不知道,而且两辆车还是在奔跑中,走过的路程也不确定,不知道如何求时间。
其实有时候,不需要我们每个概念都知道具体的数值,同样也能算出答案。对于题干条件“坐在慢车上的人见整列快车驶过的时间是4秒”来说,慢车的人看见的是快车驶过去,也就是从车头驶过到车尾出现,所以,这里走完的路程就是快车的长度:160米。那速度呢?由于两辆车是相向行驶,所以速度是快慢车速度之和。因此有:
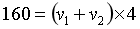
现在球的是坐在快车上的人见整列慢车驶过的时间,那么,由于还是相向行驶,所以整体速度还是快慢车速度之和。不过这里是看见慢车驶过,所以,这里所需的路程是120米。假设所需时间为t,则有:
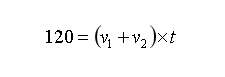
根据上述两式,易得t=3秒。因此选A。
有些同学觉得这类题不太好理解,一般都是相遇或追及问题,走过的行程是个相对确定的表达式。而这类相遇直到错过的问题,总感觉路程把握的不够牢固。如果你这样想,那老师用另一种方法讲,你就完全明白了。
还是上面这道题,“坐在慢车上的人见整列快车驶过的时间是4秒”,在这里,我们假设慢车是相对静止的,那么快车相对来说,速度就是快慢车速度之和。此时看见整列快车驶过,那走过的行程就是快车的长度160米。同样可以算出来快慢车速度之和为40米/秒。
“坐在快车上的人见整列慢车驶过”,我们这里假设快车是相对静止的,那么慢车相对快车来说,速度就是快慢车速度之和40米/秒。此时快车上的人看见慢车驶过,那走过的路程就是慢车长度120米,同样可以求得时间为3秒。
2
我们再来看一道类似的题,做完后,感受会更深一些:
(1998年)在有上下行的轨道上,两列火车相向开来,若甲车长187米,每秒行驶25米,乙车长173米,每秒行驶20米,则从两车头相遇到车尾离开,需要:
A.12秒 B.11秒 C.10秒 D.9秒 E.8秒
像这道题,我们就可以假设甲车静止,那么乙车的速度就是25+20=45米/秒。从车头相遇到车尾分离,经过的路程为187+173=360米,那么所需时间为360÷45=8秒。
3
行程问题少不了三要素:路程、速度、时间。可有的题中,提供的数据几乎只涉及到一类,比如只给了时间的数据,没有涉及其他两个,这类题怎么做呢?我们来看一道:
小张骑自行车行驶在双轨铁路旁的公路上,他注意到:每隔12分钟,就有一列火车由后面追上他,每隔4分钟,就有一列火车由对面向他开来。如果每列火车的间隔一定,速度相同,且火车和骑手都是匀速的,则火车的开车间隔为:
A.6分钟 B.5分钟 C.4分钟 D.7分钟
E.8分钟
这道题里的两个数据,都是关于时间的,所求的内容也是关于时间的。除此之外,没有其他数据了。
那这类题我们怎么做呢?答案是:该干啥干啥!我们仍然要把时间、路程、速度之间的关系建立起来。
速度方面,我们假设小张的速度是x,火车的速度是y。路程方面,题中唯一涉及到长度的,就是火车的间隔长度,由于间隔一定,速度相同,所以我们假设间隔距离为S。
分析:类似于这种不断循环的过程,我们就从这个过程的开始到结束去考察。比如这道题,我们就从现在被追上,到下一次被追上。现在相遇到下一次相遇。用周期来研究。
“每隔12分钟,就有一列火车由后面追上他”,说明火车在他后面距离为S(前车刚追上他的时候),然后用时12分钟追上他。得:
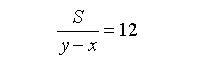
“每隔4分钟,就有一列火车由对面向他开来”,说明火车在他前面距离为S(前车刚和他碰面的时候),然后用时4分钟和他相遇。得:
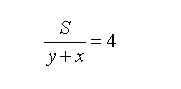
两式合并,可求得:
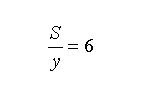
即,火车的开车间隔是6分钟。
好了,限于篇幅,这期的内容我们就先讲到这里了,下一期,我们再来几道难一些的行程问题,我们继续研究数学之美。




