应用题一般都是偏简单一些的,都是给大家的送分题,也算是发给大家的福利吧。不过有时候为了区分学生的成绩,也会在应用题中,设置一些比较难的题。这类题没有常规的套路可循,我们无法用正常的数学公式来做套,不过这类题往往和生活结合的很紧密,只要有一定的生活常识,这类题做起来就不难。今天我们就来看几道这样的题。
(2013年)福彩中心发行彩票的目的是为了筹措资金帮助福利事业,
现福彩中心准备发行一种面值为5元的福利彩票刮刮卡,
方案设计如下:①该福利彩票的中奖率为50%;
②每张中奖彩票的中奖奖金有5元和50元两种。
假设购买一张彩票获得50元奖金的概率为P,
且福彩中心筹得资金不少于发行彩票面值总和的32%,则()
A、p≤0.005 B、p≤0.01 C、p≤0.015 D、p≤0.02 E、p≤0.025
很多学生看到以后直接就懵了,这中间感觉挺复杂呀!不知道如何下手啊!其实很简单,看老师给你娓娓道来!
我们先来看下福彩中心发行彩票的整套流程:①发行彩票,回笼资金。②将中奖的资金,发到中奖人手中。③剩余资金就是筹得的资金,用于福利事业(这里不去管员工工资、五险一金、物料费等啥的哈!)。下面我们就按照这个步骤去一步步分析。
①发行彩票,回笼资金。每张彩票面值5元,不知道发行了多少张,我们就假设发行了x张吧,那么把彩票卖完,总共收到5x元,这是筹得的总钱数。
②将中奖的资金,发到中奖人手中。这里的中奖,总共分为两个档次,中5元和中50元。总的中奖率是50%,中50元的中奖率是p,那么中5元的中奖率是50%——p。
那么中5元的,总共有(50%——p)x张,总共需要兑付5x(50%——p)元。
那么中50元的,总共有px张,总共需要兑付50px元。
③剩余资金就是筹得的资金。剩余的资金等于总资金,减去兑付的资金,即5x——5x(50%——p)——50px,这就是筹得的资金。题中说筹得的资金不少于发行彩票面值总和的32%,即5x——5x(50%——p)——50px≥32%×5x。
那我们解上面的不等式,就可以算出来:p≤0.02。
上面的题,可能刚开始看的时候不太好理解,讲清楚过程后,就好明白了。下面我们来一道大家都能看明白,但容易因为理解错误而做错的题。
(2011年)某种新鲜水果的含水量为98%,
一天后的含水量降为97.5%。
某商店以每斤1元的价格购进了1000斤新鲜水果,
预计当天能售出60%,两天内售完。
要使利润维持在20%,则每斤水果的平均售价应定为()元
A、1.20 B、1.25 C、1.30 D、1.35 E、1.40
这道题的模型其实很简单,第一天卖出600斤水果,第二天卖出剩余的水果(注意!不是400斤,含水量已经发生了变化!)。然后最终利润维持在20%,也就是挣了200块钱,即卖出的钱是1200元。
那现在的关键就在于,第二天的水果变成了多少斤?那我们设第二天的水果变成了y斤吧!。有的同学只盯着含水量的变化,列出了式子400×98%=97.5%y,然后算出来y=402斤,这个答案当然是不对的,放一夜怎么会增重了呢?这个式子的问题在于,它隐含了含水的量不变(注意“的”字,这里指的是水分的量)。
含水量变化了,含的水量当然也跟着变化了。而等量关系的建立,就在于前后有不变的量,或者前后的变化有固定的差值。那在这里前后什么物质没有变化呢?水果中干物质的量没有变化(你可以理解成果干、果肉等非水分的东西)。那么第一天的干物质的含量是1——98%=2%。一天后,干物质的含量是1——97.5%=2.5%。由此,我们可以建立起等量关系式:400×2%=2.5%y,可得第二天的水果重量为y=320斤!好吓人!放了一夜,少了80斤,还不如第一天就促销卖掉呢!店老板脑子里一定会响起来(小朋友,你是否有很多问号......)。
我们假设水果售价为x,那么(600+320)x=1200,容易解得,x=1.30。
所以你看,有时候题中给你的数据,也不是直接就能用的,我们需要把这些数据转变一下或者调整一下才能顺利解题呢!
应用题其实做多了,很有意思的,因为应用题和生活的联系太紧密了,会涉及到生活中的方方面面,多做一做这类题,不但可以增长见识,还能锻炼我们的数学思维,进而锻炼我们解决问题的能力。
数学思维是理科思维,理科思维讲究什么东西都按照步骤来,就像我们的工作一样,设定好目标,分解目标,一步步执行。掌握好理科思维,能让我们做事情有条不紊,一丝不苟,这也是我们和世界建立联系的一种很好的方式。
下面,我们再来看一道题,这个和大家生活中的关系更加密切了。
(2009年)某人在市场上买猪肉,小贩称得肉重为4斤,
但此人不放心,拿出一个自备的100克重的砝码,
将肉和该砝码放在一起让小贩用原秤复称,
结果重量为4.25斤,由此可知顾客应要求小贩补猪肉()两。
A、3 B、6 C、4 D、7 E、8
这道题中涉及到了“克”和“斤”,这需要大家具备换算知识,别笑!这个还真的有学生不会的。这里简单普及一下:500克=1斤=10两。
这道题还有一点会引起争议的地方在于:小贩的秤,是按照比例虚增重量(比如固定增重20%等),还是固定增重一定重量呢(比如固定增重0.5斤)?
其实,我们用极限法就可以判断:如果固定增重一定重量,比如0.5斤,那么如果我买0.1斤肉,称出来是0.6斤,那就差6倍,差别太大,小贩除非卖给傻子才行!再说了,如果是固定增重,将砝码和猪肉称重的时候,应该显示4.2斤!
所以,这道题,增重是按照一定比例的。假设现在这块肉重量为x斤,显示出来是4斤。那么当加上砝码后,实际重量为x+0.2斤(100克为2两),显示出来是4.25斤。所以他们的比例为:
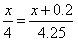
我们解得,x=3.2斤,也就是这块肉是3.2斤,小贩称出来是4斤,足足少了8两啊!都够老师炒俩菜,喝两瓶了!妥妥的奸商无疑了!黑心商家鉴定完毕!
以上就是“研线小课堂 | 那些让人头疼的应用题”的全部内容,更多考研数学备考相关内容,请持续关注!




