作为线性代数的两个核心之一的特征值与特征向量，是考研数学一和数学二、数学三的共同考试内容，常常以大题的形式出题，每年必考。所以理解特征值与特征向量的概念，熟悉与之相关的题型及解法，对于取得这部分题目的分数尤为重要。
从历年考研数学中“特征值和特征向量”的考题题型分析来看，特征值、特征向量是线性代数的重点内容，是考研的重点之一，题多分值大，共有三部分重点内容：特征值和特征向量的概念及计算、方阵的相似对角化、实对称矩阵的正交相似对角化。而2015年数一、数二、数三的一个大题又出现了两个矩阵相似和矩阵相似对角化的问题，所以今年的线性代数题目的难度下降了很多。
此章节常考题型有：
第一，数值矩阵的特征值和特征向量的求法。根据已给出矩阵，通过特征方程求出特征值，然后通过求齐次线性方程组的基础解系，求出矩阵的属于特征值的线性无关的特征向量;
第二，抽象矩阵特征值和特征向量的求法。一般利用特征值和特征向量的定义及性质;
第三，判定普通方阵的相似对角化问题。利用判定定理“n阶方阵A有n个线性无关的特征向量”或者“k重特征值恰好对应k个线性无关的特征向量”来判定;今年就考到了利用“k重特征值恰好对应k个线性无关的特征向量”来判定方阵相似对角化的问题。
第四，由特征值或特征向量反求A。一般根据题目中所给的条件转换为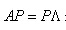
来解决;
第五，有关实对称矩阵的性质的问题。实对称矩阵的4个重要性质(1)不同特征值对应的特征向量一定正交(2)k重特征值一定对应k个线性无关的特征向量(3)实对称矩阵A一定可以相似对角化，即存在可逆矩阵P使得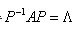
(4)存在正交矩阵Q，使得
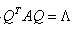。几乎每年必定会考到其中的某条或某些性质，所以一定要牢记，并熟练掌握和应用。但2015年就没有考到，所以今年出的线代题目太简单了。
