为了帮助广大考生复习好、考好数学,下面对多年来考研数学真题各个章节考点的分布规律进行了细致的分析总结,现与大家分享,供各位考生参考,希望对大家有所帮助。下面对考研数学(一)中的多元函数微分及应用部分的真题考点进行分析总结。
下面的内容包括:空间解析几何、多元函数的微分、多元函数的几何应用及多元函数的极值,这几部分内容的考点分布规律如下表所示。
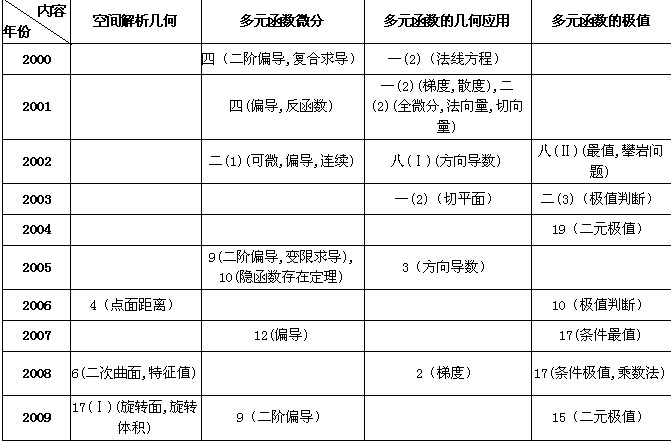
上面表格中数字表示相应年份的试卷中考题的题号,数字后面括号里的文字说明表示该考题涉及的主要考点或主要解题方法。
注:1)“最值判断”指二元函数的最大最小值的判断,“条件最值”指条件极值结合最值,2)“乘数法”指拉格朗日乘数法,3)“单调性”此处指多元函数对单变量的单调性 ,4)“抽象函数”指不是用一个具体表达式表达的函数,5)“公式法”指求偏导时利用隐函数的求导公式,6)“变限求导”指对变限积分函数求导,7)“点面距离”指点到平面的距离,8)“复合求导”指复合函数的求导。
从近15年考题特点来看,关于空间解析几何方面的内容,直接考的次数很少,只在2006年、2008年和2009年考过,其它年份都未直接出考题,这说明空间解析几何不是考试的重点,但这并不意味着以后不考,事实上,由于从2010年到2014年都未考,今后一两年内倒是很可能考,所以大家还是应该复习一下。另外,在三重积分和曲线曲面积分的有关考题中,也可能间接得考查空间解析几何的知识点。
在多元函数微分部分,主要考题题型有:求二阶偏导数、求全微分、判断函数是否可微,尤其是抽象复合函数的二阶偏导数,大家在计算时,一定要注意一阶偏导数仍然是复合函数。除了这几个题型外,有时也会考:隐函数存在定理、隐函数求偏导、多元复合函数、变积分限的函数的求导。
关于多元函数微分的几何应用,主要考查:曲面的切平面和法线、方向导数和梯度,有时可能考空间曲线的切线和法平面。
关于多元函数的极值,这是一个几乎年年考的知识点,主要题型包括:求二元函数的极值/最值和条件极值(拉格朗日乘数法)、极大值或极小值判断。
上面就是对近15年考研数学(一)中的多元函数的微分及其应用方面的真题考点和题型特点所作的总结分析,供各位考生参考,以后蔡老师还会陆续对考研数学中其它考试内容的考点和题型特点及规律进行总结分析,希望各位考生留意查看,最后祝大家数学复习顺利,考试马到成功。




