为了帮助广大考生复习好、考好数学,下面对多年来考研数学真题各个章节考点的分布规律进行了细致的分析总结,现与大家分享,供各位考生参考,希望对大家有所帮助。下面对考研数学(二)中的一元函数积分学部分的真题考点进行分析总结。
一元函数积分学包括三部分内容:不定积分、定积分、定积分的应用。这几部分内容的考点分布规律如下表所示。
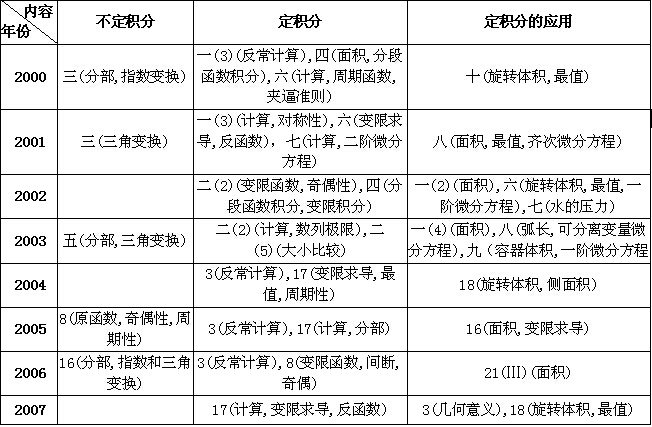
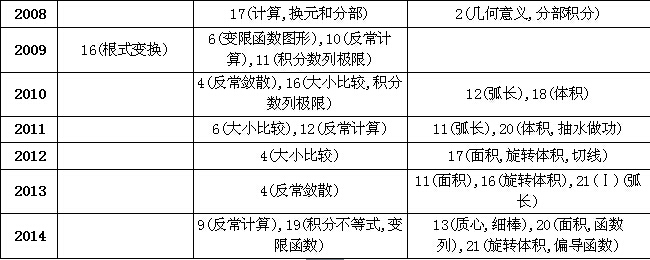
上面表格中数字表示相应年份的试卷中考题的题号,数字后面括号里的文字说明表示该考题涉及的主要考点或主要解题方法。
注:1)“计算”指定积分的计算,2)“反常计算”指反常积分的计算,3)“反常敛散”指反常积分的收敛和发散的判断,4)“分部”指分部积分法,“倒变换”指1/x=t的变换,5)“大小比较”指定积分大小的比较,6)“旋转体积”指旋转体的体积问题;7)“变限求导”指对变限积分函数求导,“变限函数”指变积分限的函数;8)“几何意义”指定积分的几何意义;9)“最值”指函数的最小值和最大值。
从近15年考题特点来看,关于不定积分的内容,直接考的次数较少,最近5年都没有直接考,在2007年之前考的频率比2007年之后的频率高,之所以不定积分考题出现的频率较低,主要有两个原因:一个原因是不定积分与定积分在计算方法上基本相同,主要采用3种方法:直接用基本积分公式、换元法和分部积分法,所以考定积分在本质上也是在考不定积分,但定积分的应用比不定积分更广泛,因而历年考定积分的频率较高,而考不定积分的频率很低;另一个原因是不定积分常常是在与其它知识点的考查过程中结合考查,比如微分方程、定积分等。求不定积分的主要方法是分部积分法和换元法,尤其是换元法;常用的换元法包括:三角变换、根式变换和指数变换等。
在定积分部分,主要考题题型有:定积分的计算、反常积分的计算、反常积分收敛性的判断、定积分大小的比较,除了这几种主要题型外,有时还会考:积分数列的极限、定积分的证明问题。定积分有时会结合夹逼准则、微分方程进行出题考查。定积分计算中的基本方法是分部积分法和换元法,换元法的具体换元形式需根据被积函数和积分区域的具体特点来选取,常用的换元形式有:三角变换、根式代换、倒代换等。在定积分问题中,还有一个非常重要的方法,就是变限积分的函数的求导,包括变上限和变下限积分的函数,这个方法不仅在积分的计算和证明中经常用到,而且在计算函数极限、微分中值问题的证明、微分方程的求解等问题中经常用到,因此,各位考生一定要熟练掌握。
关于定积分的应用,包括两个方面:几何应用和物理应用。几何应用题型包括:平面图形的面积计算、旋转体的体积和侧面积计算、曲线的弧长计算,尤其是旋转体的体积,包括平面图形绕x或y轴旋转一周,或绕平行于x或y轴的直线旋转一周的体积计算,大家一定要熟练掌握。定积分的物理应用主要是关于物体运动、做功、引力、压力、质心、形心等。在几何应用和物理应用中,几何应用考得更多。定积分的应用问题中,经常结合微分方程出题考查。
上面就是对近15年考研数学(二)的一元函数积分学内容的真题考点和题型特点所作的总结分析,供各位考生参考,以后我们还会陆续对考研数学中其它考试内容的考点和题型特点及规律进行总结分析,希望各位考生留意查看,最后祝大家数学复习顺利,考试马到成功。




